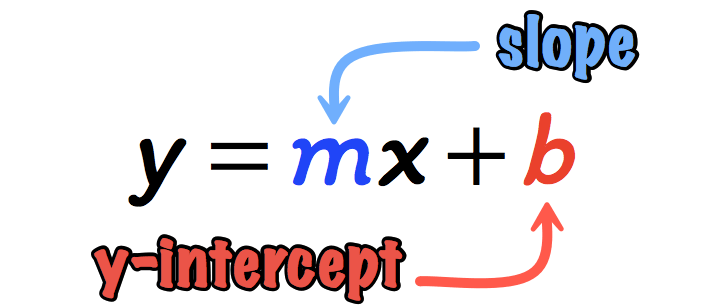
The slope-intercept is the most “popular” form of a straight line. Many students find this useful because of its simplicity. One can easily describe the characteristics of the straight line even without seeing its graph because the slope and [latex]y[/latex]-intercept can easily be identified or read off from this form.
The linear equation written in the form
is in slope-intercept form where:
[latex]m[/latex] is the slope, and [latex]b[/latex] is the [latex]y[/latex]-intercept
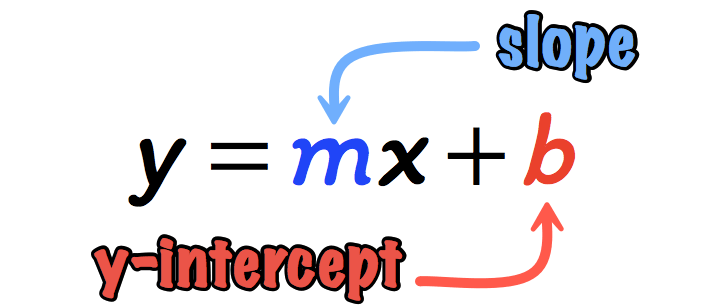
Quick notes:
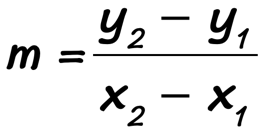
Let’s go over some examples of how to write the equation of a straight line in linear form [latex]y = mx + b[/latex].
Example 1: Write the equation of the line in slope-intercept form with a slope of [latex] – \,5[/latex] and a [latex]y[/latex]-intercept of [latex]3[/latex].
The needed information to write the equation of the line in the form [latex]y = mx + b[/latex] are clearly given in the problem since
[latex]m = – \,5[/latex] (slope)
[latex]b = 3[/latex] ([latex]y[/latex]-intercept)
Substituting in [latex]y = mx + b[/latex], we obtain
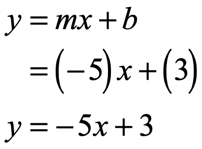
By having a negative slope, the line is decreasing/falling from left to right, and passing through the [latex]y[/latex]-axis at point [latex]\left( \right)[/latex].
Example 2: Write the equation of the line in slope-intercept form with a slope of [latex]7[/latex] and a [latex]y[/latex]-intercept of [latex] – \,4[/latex].
The slope is given as [latex]m = 7[/latex] and the [latex]y[/latex]-intercept as [latex]b = – \,4[/latex]. Substituting into the slope-intercept formula [latex]y = mx + b[/latex], we have
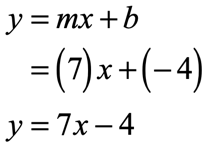7 and b=-4, we can substitute that into the slope-intercept form of a line to get y=mx+b → y=7x-4" width="206" height="146" />
The slope is positive thus the line is increasing or rising from left to right, but passing through the [latex]y[/latex]-axis at point [latex]\left( \right)[/latex].
Example 3: Write the equation of the line in slope-intercept with a slope of [latex]9[/latex] and passing through the point [latex]\left( \right)[/latex].
This problem is slightly different from the previous two examples because the [latex]y[/latex]-intercept [latex]b[/latex] is not given to us upfront. So our next goal is to somehow figure out the value of [latex]b[/latex] first.
However, if we examine the slope-intercept form, it should lead us to believe that we have enough information to solve for [latex]b[/latex]. How?
That means [latex]m = 9[/latex], and from the given point [latex]\left( \right)[/latex] we have [latex]x = 0[/latex] and [latex]y = – \,2[/latex]. Let’s substitute these known values into the slope-intercept formula and solve for the missing value of [latex]b[/latex].
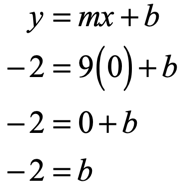
Now it is possible to write the slope-intercept form as
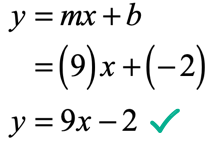
Example 4: Find the slope-intercept form of the line with a slope of [latex] – \,3[/latex] and passing through the point [latex]\left( < – 1,\,15>\right)[/latex].
Again, the value of [latex]y[/latex]-intercept [latex]b[/latex] is not directly provided to us. But we can utilize the given slope and a point to find it.
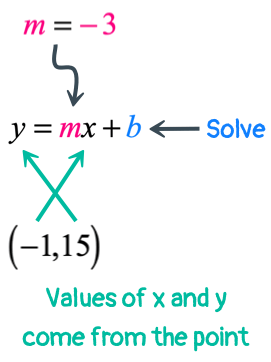
Substitute the known values into the slope-intercept formula, and then solve for the unknown value of [latex]b[/latex].
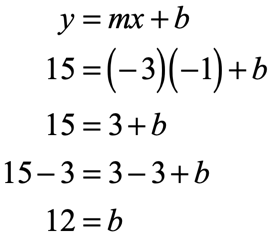
Back substitute the value of the slope and the solved value of the [latex]y[/latex]-intercept into [latex]y = mx + b[/latex].
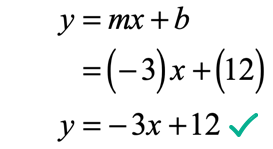
Example 5: A line with the slope of [latex] – \,8[/latex] and passing through the point [latex]\left( < – \,4,\, – 1>\right)[/latex].
The given slope is [latex]m = – \,8[/latex] and from the given point [latex]\left( < – \,4,\, – 1>\right)[/latex], we have [latex]x = – \,4[/latex] and [latex]y = – \,1[/latex]. Now, we are going to substitute the known values into the slope-intercept form of the line to solve for [latex]b[/latex].
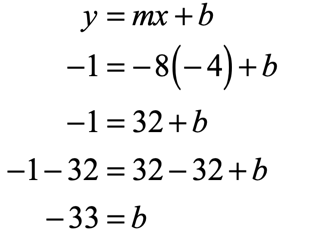
Since [latex]m = – \,8[/latex] and [latex]b = – \,33[/latex], the slope-intercept form of the line becomes
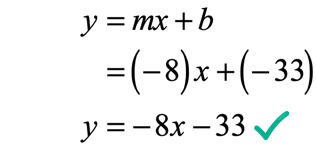
Example 6: Write the slope-intercept form of the line with a slope of [latex][/latex] and through the point [latex]\left( \right)[/latex].
We have a slope here that is not an integer, i.e. the denominator is other than positive or negative one, [latex] \pm 1[/latex]. In other words, we have a “true” fractional slope.
The procedure for solving this problem is very similar to examples #3, #4, and #5. But the main point of this example is to emphasize the algebraic steps required on how to solve a linear equation involving fractions.
The known values of the problem are
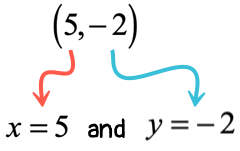
Plug the values into [latex]y = mx + b[/latex] and solve for [latex]b[/latex].
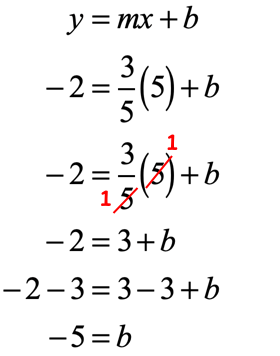
As you can see the common factors of [latex]5[/latex] in the numerator and denominator nicely cancel each other out which greatly simplifies the process of solving for [latex]b[/latex].
Putting this together in the form [latex]y = mx + b[/latex]
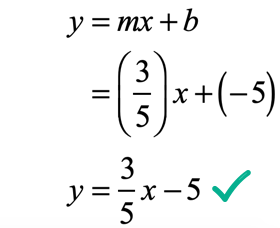
Example 7: Slope of [latex] \over 2>[/latex] and through the point [latex]\left( < – 1,\, – 1>\right)[/latex].
The given slope is [latex]m = \over 2>[/latex] and from the given point [latex]\left( < – 1,\, – 1>\right)[/latex], the values of [latex]x[/latex] and [latex]y[/latex] can easily be identified.
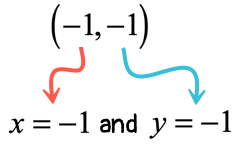
Now plug in the known values into the slope-intercept form [latex]y = mx + b[/latex] to solve for [latex]b[/latex].
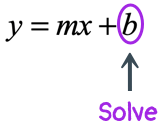
Make sure that when you add or subtract fractions, you generate a common denominator.
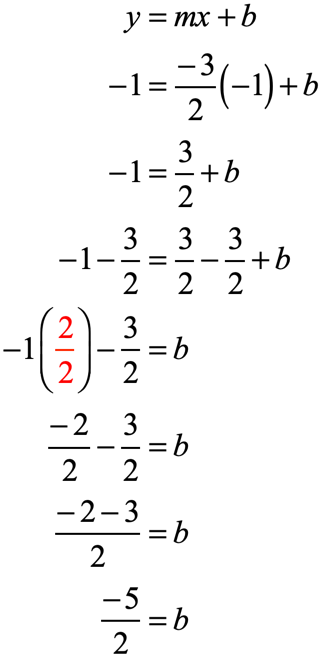
After getting the value of [latex]b[/latex], we can now write the slope-intercept form of the line.
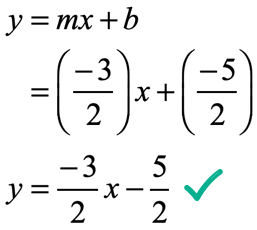
Example 8: Slope of [latex] – \,6[/latex] and through the point [latex]\left( ,> \right)[/latex].
The slope is given as [latex]m = – \,6[/latex] and from the point, we have [latex]x = [/latex] and [latex]y = [/latex].
Substitute the known values into [latex]y = mx + b[/latex]. Then solve the missing value of [latex]b[/latex] .
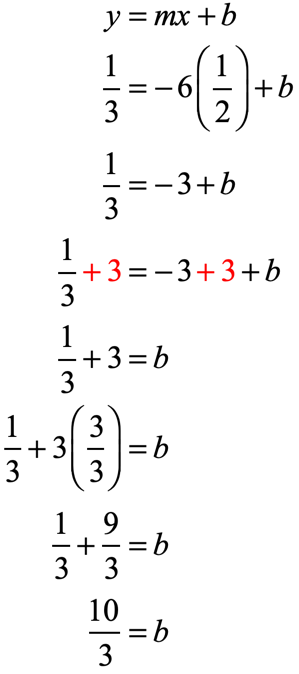
Therefore, the slope-intercept form of the line is
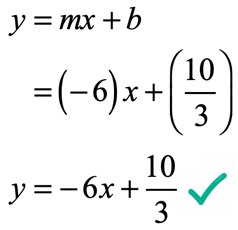
Example 9: Slope of [latex] \over 3>[/latex] and through the point [latex]\left( \over 5>,> \right)[/latex].
Identifying the known values
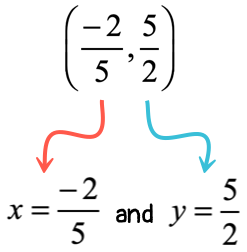
The setup to find [latex]b[/latex] becomes
That makes the slope-intercept form of the line as
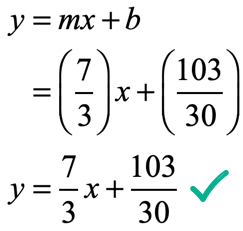
Example 10: A line passing through the given two points [latex]\left( \right)[/latex] and [latex]\left( \right)[/latex].
In this problem, we are not provided with both the slope [latex]m[/latex] and [latex]y[/latex]-intercept [latex]b[/latex]. However, we should realize that the slope is easily calculated when two points are known using the Slope Formula.
The slope, [latex]m[/latex], of a line passing through two arbitrary points [latex]\left( ,> \right)[/latex] and [latex]\left( ,> \right)[/latex] is calculated as follows…
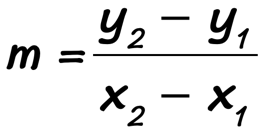
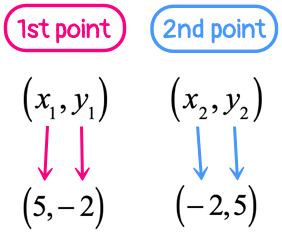
If we let [latex]\left( \right)[/latex] be the first point, then [latex]\left( \right)[/latex] must be the second.
Labeling the components of each point should help in identifying the correct values that would be substituted into the slope formula.
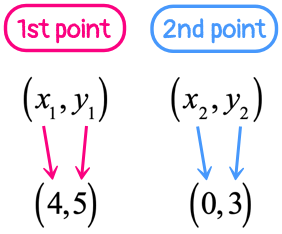
Based on the labeling above, now we know that
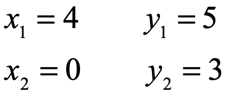
Next, write the slope formula, plug in the known values and simplify.
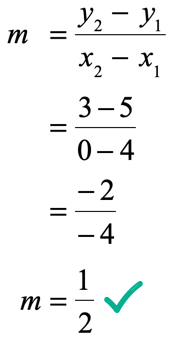
Great! We found the slope to be [latex]m = \over 2>\,[/latex]. The only missing piece of the puzzle is to determine the [latex]y[/latex]-intercept. Use the slope that we found, together with ANY of the two given points. In this exercise, I will show you that we should arrive at the same value of the [latex]y[/latex]-intercept regardless of which point is selected for the calculation.
Finding the [latex]y[/latex]-intercept
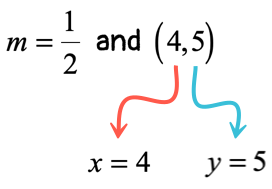
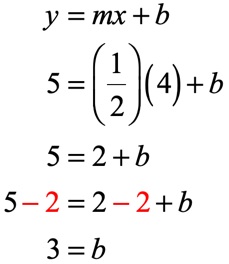
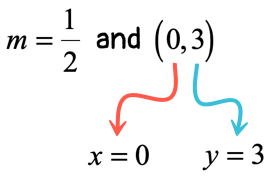
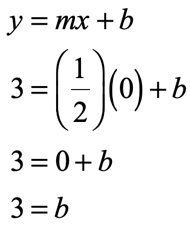
Indeed, the [latex]y[/latex]-intercepts come out the same in both calculations. We can now write the linear equation in slope-intercept form.
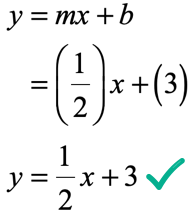
Below is the graph of the line passing through the given two points.
Example 11: A line passing through the given two points [latex]\left( < – \,7,\,4>\right)[/latex] and [latex]\left( < – \,2,\,19>\right)[/latex].
Let’s solve this step by step.
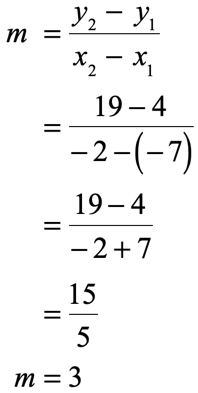
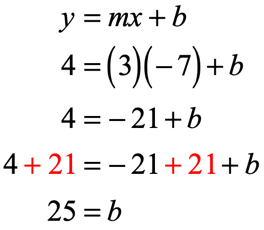
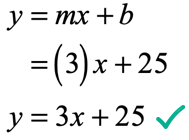
Example 12: A line passing through the given two points [latex]\left( < – \,6,\, – \,3>\right)[/latex] and [latex]\left( < – \,7,\, – 1>\right)[/latex].
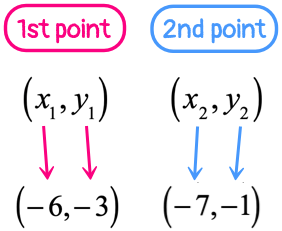
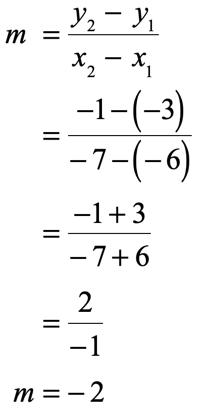
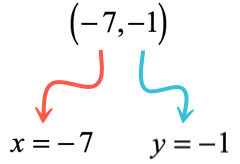
Substitute known values in the slope-intercept form [latex]y = mx + b[/latex] to solve for [latex]b[/latex].
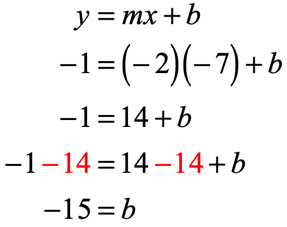
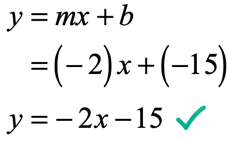
Example 13: A line passing through the given two points [latex]\left( \right)[/latex] and [latex]\left( < – \,2,\,5>\right)[/latex].
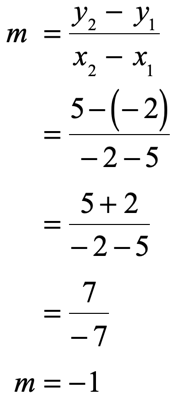
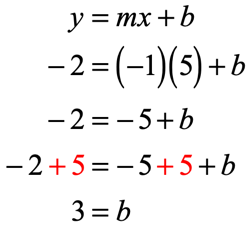
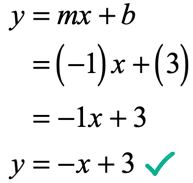
You might also like these tutorials:
Categories
